- trigonometry, 삼각법
- trigonometric ratio, 삼각비
- trigonometric functions, 삼각함수
- 삼각함수의 성질
정의
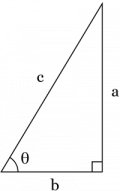
삼각비
| 사인 | <math>\sin\theta=\frac{a}{c}</math> | 코시컨트 | <math>\csc\theta=\frac{c}{a}=\frac{1}{\sin\theta}</math> |
| 코사인 | <math>\cos\theta=\frac{b}{c}</math> | 시컨트 | <math>\sec\theta=\frac{c}{b}=\frac{1}{\cos\theta}</math> |
| 탄젠트 | <math>\tan\theta=\frac{a}{b}</math> | 코탄젠트 | <math>\cot\theta=\frac{b}{a}=\frac{1}{\tan\theta}</math> |
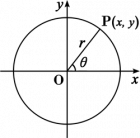
삼각함수
| 사인 | <math>\sin\theta=\frac{y}{r}</math> | 코시컨트 | <math>\csc\theta=\frac{r}{y}=\frac{1}{\sin\theta}</math> |
| 코사인 | <math>\cos\theta=\frac{x}{r}</math> | 시컨트 | <math>\sec\theta=\frac{r}{x}=\frac{1}{\cos\theta}</math> |
| 탄젠트 | <math>\tan\theta=\frac{y}{x}</math> | 코탄젠트 | <math>\cot\theta=\frac{x}{y}=\frac{1}{\tan\theta}</math> |
성질
- <math>\tan\theta=\frac{\sin\theta}{\cos\theta}</math>
θ+90°
- <math>\sin(\theta+\frac{\pi}{2})=\cos\theta</math>
- <math>\cos(\theta+\frac{\pi}{2})=-\sin\theta</math>
- <math>\tan(\theta+\frac{\pi}{2})=-\frac{1}{\tan\theta}</math>
θ+180°
- <math>\sin(\theta+\pi)=-\sin\theta</math>
- <math>\cos(\theta+\pi)=-\cos\theta</math>
- <math>\tan(\theta+\pi)=\tan\theta</math>
θ+360°
<math>n</math>이 정수일 때
- <math>\sin(\theta+2n\pi)=\sin\theta</math>
- <math>\cos(\theta+2n\pi)=\cos\theta</math>
- <math>\tan(\theta+2n\pi)=\tan\theta</math>
-θ
- <math>\sin(-\theta)=-\sin\theta</math>
- <math>\cos(-\theta)=\cos\theta</math>
- <math>\tan(-\theta)=-\tan\theta</math>
90°-θ
- <math>\sin(\frac{\pi}{2}-\theta)=\cos\theta</math>
- <math>\cos(\frac{\pi}{2}-\theta)=\sin\theta</math>
- <math>\tan(\frac{\pi}{2}-\theta)=\frac{1}{\tan\theta}</math>
180°-θ
- <math>\sin(\pi-\theta)=\sin\theta</math>
- <math>\cos(\pi-\theta)=-\cos\theta</math>
- <math>\tan(\pi-\theta)=-\tan\theta</math>